МЕТОД СИМПСОНА ДЕЛФИ

Метод Симпсона является численным алгоритмом интегрирования функций и является частным случаем метода трапеций. Данный метод является более точным и позволяет получать более точные результаты, чем метод трапеций.

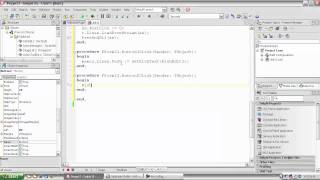
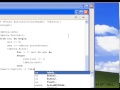
Метод Симпсона делфи представлен в стандартной библиотеке языка программирования Delphi. Для использования данной функции необходимо правильно задать параметры функции, которую необходимо проинтегрировать. Пример использования метода Симпсона для интегрирования функции f(x) на интервале [a,b] представлен в следующем коде:

function simpson(f: TFunc; a,b: Double; n: Integer): Double;var h,x,sum: Double; i: Integer;begin if (n mod 2 = 1) then raise Exception.Create('n должно быть четным'); h := (b-a)/n; x := a+h; sum := 0; for i:=1 to n div 2 do begin sum := sum + 4*f(x); x := x + 2*h; end; x := a + 2*h; for i:=1 to (n div 2)-1 do begin sum := sum + 2*f(x); x := x + 2*h; end; Result := (h/3)*(f(a) + f(b) + sum);end;

В данном примере функция simpson принимает на вход функцию f, которую необходимо проинтегрировать, значения пределов интегрирования a и b и количество разбиений n. Результатом выполнения функции является значение интеграла функции f(x) на интервале [a,b].

Численное интегрирование: Методы Левых Правых прямоугольников, Трапеций, Симпсона c++

Лекция 160: Формула Симпсона (парабол)

Как сделать нейросеть в Delphi

Формула Симпсона

Delphi Technique

Английский для тестировщиков с Асей Перельцвайг - урок №1